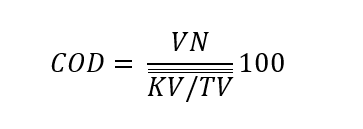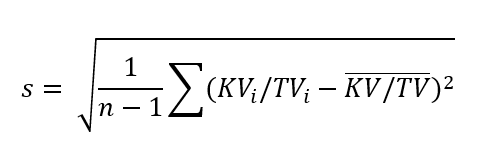Publicēts: 14.10.2020.

Valsts zemes dienests ik gadu, kadastrālās vērtēšanas ietvaros, veic aprēķināto kadastrālo vērtību un tirgus cenu atbilstības novērtējumu – gan tādēļ, lai noskaidrotu teritorijas un īpašumu grupas, kurām nepieciešamas izmaiņas kadastrālo vērtību bāzes rādītājos (bāzes vērtības, standartapjomi, korekcijas koeficienti) nākošajam periodam, gan tādēļ, lai novērtētu iegūtos rezultātus kadastrālo vērtību bāzes izstrādes laikā un izlemtu, vai iegūto rezultātu virzīt apstiprināšanai Ministru kabinetā vai to koriģēt un uzlabot.

Savā darbībā, novērtējot kadastrālās vērtēšanas rezultātus, Valsts zemes dienests vadās pēc starptautiskās vērtētāju asociācijas (IAAO – International Association of Assessing Officers) standartiem, kuri apraksta aprēķināto masveida vērtību un tirgus vērtību attiecību analīzi (Standard on Ratio Studies).

Gan individuāla īpašuma vērtēšana, gan masveida vērtēšana, kas Latvijā pazīstama kā kadastrālā vērtēšana, sastāv no vieniem un tiem pašiem posmiem, un abos vērtēšanas veidos īpašuma vērtības noteikšanai tiek izmantotas izmaksu, darījumu salīdzināšanas un ienākumu kapitalizācijas metodes. Tomēr vērtētāji, kas nodarbojas ar masveida vērtēšanu, izstrādā vērtēšanas modeļus, kas tiek pielietoti īpašuma grupu un nevis viena īpašuma vērtēšanā. Atšķirībā no starptautiskās pieredzes, Latvijā vērtēšanas modeļi tiek apstiprināti ar Ministru kabineta noteikumiem un, lai tos izmainītu un uzlabotu kadastrālo vērtību atbilstību nekustamā īpašuma tirgus situācijai, ir jāizdara grozījumi normatīvajos aktos, kā rezultātā nav iespējams ātri reaģēt uz modeļu izmaiņu nepieciešamību.

Tāpat vērtējumu kvalitātes kontrole abos vērtēšanas veidos – individuālajā un masveida (kadastrālā) – tiek veikta atšķirīgos veidos. Viena īpašuma vērtēšanas gadījumā par vērtējuma ticamību parasti var spriest pēc tirgus situācijas izpētes un veiktās analīzes dziļuma, kā arī salīdzinot iegūto tirgus vērtību ar savstarpēji salīdzināmu darījumu datiem. Masveida vērtēšanas gadījumā vērtējumu precizitātes un saskaņotības novērtēšanai tiek izmantotas statistiskās metodes.

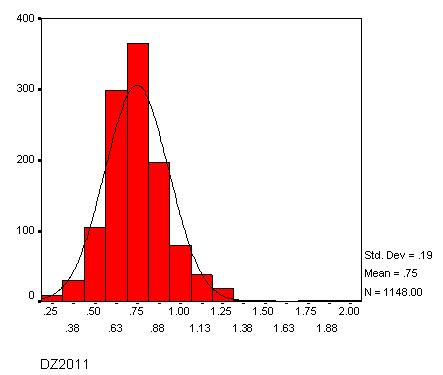
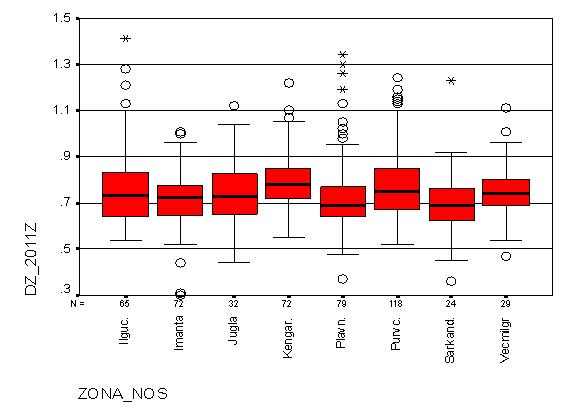
Lai novērtētu masveida vērtēšanas rezultātus, tiek veikta aprēķināto kadastrālo vērtību un tirgus cenu attiecību analīze. Par rezultātiem var spriest pēc vērtību (vērtējumu) līmeņa un vērtību vienotības.

Vērtību līmenis attiecināms uz vispārēju kadastrālo vērtību un tirgus cenu attiecību līmeni. Ņemot vērā masveida vērtēšanas specifiku nevar gaidīt, ka kadastrālās vērtības sakritīs ar ikviena īpašuma tirgus vērtību, taču augstām un zemām kadastrālo vērtību un tirgus cenu attiecībām vajadzētu būt līdzsvarā tā, lai tipiskā kadastrālās vērtību un tirgus cenu attiecība būtu tuvu 1.

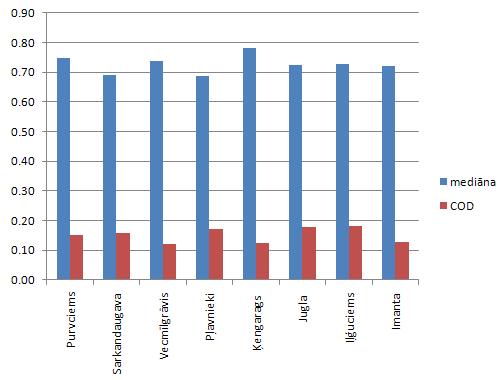
Vērtību vienotība raksturo, pirmkārt, īpašumu vērtēšanas objektivitāti katras grupas (izmantošanas veida, mikrorajona utt.) ietvaros un, otrkārt, visu īpašumu grupu novērtējuma līmeni. Vērtību vienotības sasniegšanai ir nepieciešama vērtību izlīdzināšana grupu ietvaros un starp grupām.

Vērtību vienotību dažādu īpašuma grupu starpā var novērtēt, salīdzinot vērtību līmeņus. Lielas vērtību līmeņa atšķirības norāda uz vērtību nevienlīdzību starp šīm grupām. Vērtību vienotību īpašumu grupu starpā var analizēt, izmantojot vērtību horizontālo un vertikālo vienlīdzību.

Horizontālā vienlīdzība ir saistīta ar vērtību līmeņu salīdzināšanu starp dažādām īpašumu grupām, kurās īpašumi sadalīti pēc to veida, atrašanās vietas, vecuma, platības vai kāda cita parametra.

Vertikālā vienlīdzība ir saistīta ar vērtību līmeņu saskanīgumu, vadoties pēc vērtību amplitūdas.

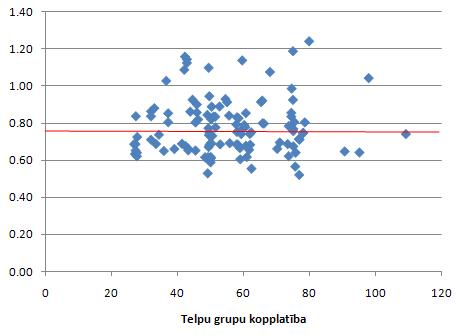
Jāņem vērā, ka kadastrālo vērtību un tirgus cenu attiecību analīzes precizitāte un ticamība ir atkarīga no analīzē izmantoto pirkuma darījumu daudzuma un kvalitātes. Nepietiekams pirkuma darījumu skaits var ietekmēt analīzes rezultātus. Tāpat jāņem vērā aspekts, ka Valsts zemes dienests nedrīkst patvaļīgi mainīt vērtēšanas modeļus, lai sasniegtu lielāku vērtību vienotību katras grupas ietvaros, jo visi vērtēšanas modeļi ir apstiprināti ar normatīvajiem aktiem.

Iespējams kadastrālo vērtību un tirgus cenu sakarību analīzes statistiskie rādītāji cilvēkiem, kuriem nav plašas zināšanas matemātikā, var šķist mulsinoši. Tāpēc tiek veidoti arī grafiki un diagrammas, kas palīdz izskaidrot kadastrālo vērtību un tirgus cenu attiecību analīzes statistiskos rādītājus un bieži sniedz arī pilnīgāku ainu par vērtēšanas rezultātiem.

Histogramma ir datu biežuma sadalījuma stabiņveida diagramma. Stabiņu augstums vai laukums attēlo katrā intervālā ietilpstošo attiecību skaitu vai procentuālo daudzumu. Augstākais stabiņš attēlo visbiežāk sastopamo vērtību attiecību (vērtējumu) līmeni, sadalījuma blīvums atspoguļo vērtību vienotību.

Histogramma arī atspoguļo kādā mērā attiecības atbilst normālajam sadalījumam, šī informācija ir svarīga kadastrālo vērtību un tirgus cenu attiecību analīzē iegūto statistisko rādītāju interpretācijai. 1.attēlā redzama vērtību attiecību histogramma, kurai pievienota normālā sadalījuma līkne.

Vērtību attiecību histogramma Rīgas pilsētā

Datu sadalījums ar pārtraukuma punktiem vai nesimetrisks datu sadalījums norāda uz nevēlamu nelīdzsvarotību starp pārāk augstiem un pārāk zemiem vērtējumiem. Ar histogrammu palīdzību var konstatēt arī neiederīgos datus, kādi ir sagaidāmi ikvienā kadastrālo vērtību un tirgus vērtību attiecību sakarību analīzē.

Kadastrālo vērtību un tirgus cenu attiecību analīzes statistiskie rādītāji sniedz koncentrētus vērtēšanas rezultātu mērus un bieži kalpo par pamatu kadastrālo vērtību bāzes rādītāju pārskatīšanai, lai veiktu vērtību izlīdzināšanu. Šī iemesla dēļ ir svarīgi, lai šie statistiskie rādītāji tiktu pareizi aprēķināti un interpretēti.

Vērtību līmeņa aprēķini ir balstīti uz centrālās tendences mēriem. Trīs no šādiem mēriem, kas ir pielietojami kadastrālo vērtību un tirgus cenu attiecību analīzē, ir mediāna, vidējā vērtība un vidējā svērtā vērtība.

Mediānai kadastrālo vērtību un tirgus cenu attiecību analīzē ir vairākas priekšrocības, proti, to neietekmē minimālās un maksimālās attiecības, kā arī to salīdzinājumā ar vidējo un vidējo svērto vērtību minimāli ietekmē datu kļūdas.

Balstoties uz mediānu tiek aprēķināts dispersijas koeficients (COD), kas ir galvenais vērtību vienotības mērs. Mediāna tiek noteikta kā sakārtotas datu kopas vidējais elements, savukārt vidējo vērtību nosaka saskaitot visas datu kopas vērtības un izdalot ar vērtību skaitu un vidējo svērto vērtību nosaka katrai attiecībai piemērojot atbilstošus svarus.

Vidējās svērtās vērtības trūkums ir tās jūtīgums pret datu kopas kļūdām, piemēram, gadījumos, kad datu kopa satur vairākus augsti novērtētus īpašumus ar salīdzinoši zemām vai augstām kadastrālo vērtību un tirgus vērtību attiecībām.

Katram no šiem aprakstītajiem rādītājiem ir savas priekšrocības un trūkumi, tāpēc ir noderīgi aprēķināt visus trīs minētos centrālās tendences mērus. To salīdzinājums sniedz noderīgu informāciju par attiecību sadalījumu. 1.tabulā ir redzami centrālās tendences mēri vērtību attiecībām Rīgas pilsētā.

Mediāna 0,73
Vidējā vērtība 0,75
Vidējā svērtā vērtība 0,70
Attiecību skaits 1148

Tabulā redzamā nelielā centrālās tendences mēru atšķirība liecina par attiecību simetrisku sadalījumu.

Masveida vērtēšanas kvalitātes noteikšanai izmanto vērtību vienotību: vienotību starp īpašumu grupām, kā arī vienotību grupu ietvaros. Vērtību vienotību starp grupām var novērtēt, salīdzinot katrai īpašumu grupai aprēķinātos vērtību līmeņa mērus. Vērtību vienotības novērtēšana īpašumu grupu ietvaros ir sarežģītāka.

Pie nelieliem datu izlašu apjomiem vērtību vienotību var noteikt apskatot analizējamo datu kopu. Lielāku izlašu gadījumā tas vairs nav iespējams, tāpēc, lai noteiktu vērtību vienotības pakāpi, ir jāaprēķina datu izkliedes mēri. Var izmantot sekojošus izkliedes mērus:

  • amplitūdu, kvartīles un procentīles;
  • dispersijas koeficientu (COD);
  • variācijas koeficientu (COV).

Amplitūda, kvartīles un procentīles

Amplitūda, kvartīles un procentīles sniedz atbalsta punktus, kas raksturo datu kopas sadalījumu. Amplitūda ir starpība starp datu kopas maksimālo un minimālo vērtību. Liela amplitūda var norādīt uz sliktu vērtību vienotību, taču tā kā amplitūda ir balstīta tikai uz zemākajām un augstākajām vērtībām, šis statistiskais rādītājs var izrādīties maldinošs vispārējās vērtību vienotības indikators.

Vērtību attiecību amplitūda Rīgas pilsētā ir 1.73

Procentīles un kvartīles ir pieaugošā secībā sakārtotas datu kopas sadalošie punkti. Kvartīles ir datu kopas vērtības, kas sakārtotu datu kopu sadala 4 vienādās daļās, savukārt procentīles ir datu kopas vērtības, kas sakārtotu datu kopu sadala 100 vienādās daļās. Pirmā kvartīle atbilst 25. procentīlei, un tā pārsniedz vienu ceturtdaļu jeb 25 procentus kadastrālo vērtību un tirgus vērtību attiecību un līdzīgi trešā kvartīle atbilst 75. procentīlei, un tā pārsniedz trīs ceturtdaļas jeb 75 procentus kadastrālo vērtību un tirgus vērtību attiecību.

Ir izstrādāti vairāki uz kvartīlēm un procentīlēm balstīti vērtību vienotības mēri. Starpkvartīļu amplitūda ir starpība starp trešo un pirmo kvartīli. Iepriekš apskatītajai datu kopai (vērtību attiecības Rīgas pilsētā), pirmā kvartīle ir 0.63, trešā kvartīle ir 0.84 un starpkvartīļu amplitūda, kurā atrodas 50% kadastrālo vērtību un tirgus cenu attiecību, ir 0.21 (0.84 – 0.63).

Citu vērtību vienotības mēru, piemēram, koncentrācijas koeficientu, var noteikt, aprēķinot noteiktā apgabalā ap mediānu ietilpstošo kadastrālo vērtību un tirgus vērtību attiecību procentuālo daudzumu. Pieļaujamajam procentuālajam daudzumam vajadzētu atbilst pieņemtajai vērtēšanas kļūdas pakāpei, piemēram, 15 procentiem. Šādā veidā aprēķinātais koncentrācijas koeficients iepriekš apskatītajai datu kopai ir 56.6, jo 650 no 1148 kadastrālo vērtību un tirgus cenu attiecībām ietilpst 15 procentu apgabalā no mediānas (starp 0.62 un 0.84). Jo lielāka ir koncentrācijas koeficienta vērtība, jo datu vienotība ir labāka.

Kvartīles, procentīles un ar tām saistītie statistiskie rādītāji var būt noderīgi, taču tie nesniedz informāciju par vērtību vienotības pakāpi ārpus izvēlētajiem atbalsta punktiem

Dispersijas koeficients (Coeffiecient of Dispersion)

Dispersijas koeficients(COD) ir visplašāk izmantotais vērtību vienotības mērs. Tas ir balstīts uz vidējo novirzi (VN), ar kuras palīdzību tiek noteikta kadastrālo vērtību un tirgus cenu attiecību vidējā absolūtā starpība no mediānas. Matemātiski vidējo novirzi var aprakstīt ar formulu:

Vidējās novirzes formula

COD izsaka vidējo novirzi procentos. Tādējādi tas sniedz vērtību vienotības mēru, kas ir neatkarīgs no vērtību līmeņa un ļauj savstarpēji salīdzināt īpašumu grupas.

COD tiek aprēķināts, absolūto novirzi izdalot ar mediānu un iegūto rezultātu sareizinot ar 100, lai pārveidotu to procentos:

Vidējās novirzes procentos formula

Zema COD (≤15.0) vērtība tiek saistīta ar labu vērtību vienotību. Reti sastopami gadījumi, kad COD <  5.0.

Vidējās novirzes koeficients vērtību attiecībām Rīgas pilsētā ir 0.14 un COD = 18.8.

 

Variācijas koeficients (Coefficient of Variation)

Variācijas koeficients (COV) ir standartnovirze, izteikta procentos. Kadastrālo vērtību un tirgus cenu attiecību analīzē tas tiek aprēķināts, standartnovirzi izdalot ar attiecību vidējo vērtību un rezultātu pareizinot ar 100:

Variācijas koeficents

Standartnovirzes aprēķina matemātiskā formula ir:

Standartnovirzes formula

Tā kā rezultāts ir procentos, tad gan COV, gan COD, var izmantot, lai salīdzinātu dažādu īpašumu grupas ar atšķirīgiem vērtību līmeņiem.

COV interpretācija balstās uz pieņēmumu par attiecību normālu sadalījumu. Ja dati ir sadalīti atbilstoši normālajam sadalījumam, tad spēkā ir tabulā redzamās sakarības.

COV skaits no vidējās vērtības Datu procentuālais daudzums
+ / - 1 68%
+ / - 2 95%
+ / - 3 99%

Piemēram, ja Rīgas pilsētā vērtību attiecību vidējā vērtība ir 0.75 (standartnovirze – 0.19, COV ir 25.0, tad 68% kadastrālo vērtību un tirgus cenu attiecību ietilps apgabalā ap vidējo vērtību, kurai pieskaitīts vai atņemts viens COV, t.i., 68% kadastrālo vērtību un tirgus vērtību attiecību būs starp 0.56 un 0.94. Ja datu sadalījums atbilst normālajam sadalījumam, tad COV ir spēcīgs vērtību vienotības mērs.

Zona Analizējamās attiecības Mediāna Vidējā vērtība Vidējā svērtā vērtība COD COV
Purvciems 118 0.75 0.78 0.75 15.2 19.3
Sarkandaugava 24 0.69 0.70 0.67 15.8 23.9
Vecmilgrāvis 29 0.74 0.75 0.74 12.2 17.2
Pļavnieki 79 0.69 0.74 0.71 17.1 24.5
Ķengarags 72 0.78 0.80 0.78 12.3 16.4
Jugla 32 0.72 0.74 0.71 18.0 22.9
Iļģuciems 65 0.73 0.77 0.75 18.2 23.4
Imanta 72 0.72 0.71 0.69 12.6 18.2
Attiecību analīzes grafiskais piemērs

 

Saskaņā ar starptautisko praksi, katrai no lielākajām īpašuma grupām vajadzētu iekļauties 5% robežā no kopējā vērtību līmeņa administratīvajā teritorijā. Tādējādi, ja kopējais vērtību attiecību vērtību līmenis Rīgas pilsētā ir 0.73 (mediāna), tad katras īpašumu grupas un zonas attiecību vērtību līmenim vajadzētu būt starp 0.69 un 0.77.

Šis vērtēšanas rezultātu aspekts ir ļoti svarīgs, jo tas ir saistīts ar sistemātisku vērtību vienlīdzību (vai tās trūkumu) starp dažādām īpašuma grupām. Tāpat, saskaņā ar starptautisko praksi, dzīvojamo īpašumu gadījumā COD vajadzētu būt ≤15.0 (jāņem vērā, ka citās valstīs COD rēķina pret vērtību „1”).

4.tabulā norādītais vērtību līmenis Rīgas pilsētas mikrorajonu griezumā ir no 0.69 līdz 0.78, kas liecina par labu vērtību vienotību starp mikrorajoniem. Savukārt dispersijas koeficients (COD) svārstās robežās no 12.2 līdz 18.2, kas arī ir samērā tuvu vēlamajam rezultātam.

Kastveida diagrammas (Box plot) var izmantot vērtību attiecību grafiskai attēlošanai. Kastes atspoguļo datu starpkvartīļu amplitūdu (starpība starp trešo un pirmo kvartīli). Kastes iekšpusē redzamās tumšās horizontālās līnijas ir mediānas. Kastveida diagrammas ir ļoti labs līdzeklis neiederīgo datu konstatēšanai. Ar aplīšiem un zvaigznītēm tiek apzīmēti attiecīgi izlecēji (neiederīgie dati) un ekstremālās vērtības (ekstrēmi) un vērtētājiem katra šāda datu kopas elementa iederību analizējamajā datu kopā atsevišķi jāizskata. Mediānu un kastu izvietojums liecina par vērtību līmeņu vienlīdzību starp grupām.

Attiecību analīzes rezultātu grafiskais piemērs atsevišķos Rīgas pilsētas mikrorajonos

Attiecību analīzes rezultātu grafiskais piemēr

Attēlā redzamā situācija liecina par labu vērtību vienotību starp mikrorajoniem

Izkliedes diagrammas (scaterrplot) ir efektīvs līdzeklis kadastrālo vērtību un tirgus cenu attiecību salīdzināšanai ar kvantitatīvo mainīgo (piemēram, dzīvokļa platība, zemesgabala platība, ēkas vecums) palīdzību. Kadastrālo vērtību un tirgus cenu attiecības tiek attēlotas uz vertikālās ass, un interesējošie kvantītatīvie mainīgie tiek attēloti uz horizontālās ass. Punktu izvietojums norāda uz vērtību objektivitāti visā interesējošā kvantitatīvā mainīgā vērtību diapazonā. Sistemātisks augšupvērsts vai lejupvērsts punktu izvietojums norāda uz vērtību nevienlīdzību (neobjektīvas vērtības).

4.attēlā diagrammas veidā ir parādītas kadastrālo vērtību un tirgus cenu attiecības vienā no Rīgas pilsētas mikrorajoniem attiecībā pret telpu grupu kopplatību, ar sarkano līniju apzīmēta mediāna. Attēlā redzamais punktu izvietojums neuzrāda nekādu augšupvērstu vai lejupvērstu punktu izvietojuma tendenci, kas liecina, ka telpu grupas kā ar mazām, tā ar lielām platībām ir novērtētas līdzvērtīgi.

Vērtību attiecību izkliedes diagrammas piemērs Purvciemā

Vērtību attiecību izkliedes diagrammas piemērs

Vairumā pasaules valstu, kurā darbojas tirgus ekonomikas principi un kurā ir uz nekustamo īpašumu tirgu balstīta masveida vērtēšana, nav sagaidāms, ka ikviena īpašuma masveida vērtēšanas procesā noteiktā (kadastrālā) vērtība sakritīs ar tā tirgus vērtību.

Jāsaprot, ka vērtēšanas procesi ir atšķirīgi un masveida vērtēšanā netiek apskatīts katrs individuālais objekts, bet gan īpašumu grupa kopumā. Tāpat jāsaprot, ka masveida vērtēšanas procesā, aprēķinot vērtību, nav iespējams ņemt vērā pilnīgi visus ietekmējošos faktorus, kas varētu ietekmēt īpašuma vērtību, kā to var izdarīt individuālās vērtēšanas gadījumā, jo, izvērtējot visus ietekmējošos faktorus, masveida vērtēšanas izmaksas, apkopojot informāciju, kļūtu nesamērojamas ar iegūto rezultātu.

Būtiskākais, kas jāpanāk masveida vērtēšanas laikā, ir vērtību vienotība katras īpašumu grupas ietvaros, kā arī vienots vērtējumu līmenis starp dažādām īpašumu grupām un teritorijām. Uzlabot situāciju var, pilnveidojot vērtēšanas modeļus, kā arī reģistrējot un aktualizējot vērtēšanai nepieciešamos datus Kadastra informācijas sistēmā.

Objektīvas kadastrālās vērtības var kalpot par pamatu izsvērtas nekustamā īpašuma nodokļa politikas izstrādei, kā rezultātā iespējams aprēķināt samērojamus, sabalansētus un taisnīgus nekustamā īpašuma nodokļus.